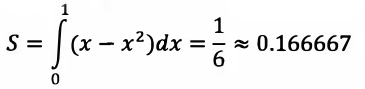Вычисление пло­щади фигуры, ограниченной двумя кривыми с помощью Python

Следующий пример, который мы рассмотрим - задача о вычислении площади фигуры, ограниченной двумя кривыми. Здесь, в этом примере, мы используем вложенные операторы цикла(то есть один оператор цикла вызывается в теле другого оператора цикла).

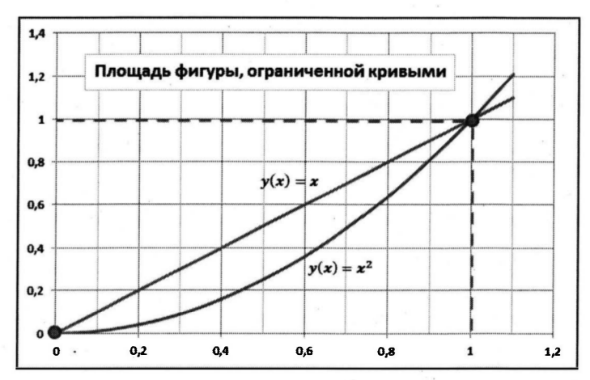
Что касается непосредственно решаемой задачи, то нам предстоит вычислить площадь фигуры, которая ограничена двумя кривыми, уравнения которых y(x) = x и y(x) = x^2. Графики этих кривых представлены на рис. 1.

Это прямая линия и парабола. Кривые пересекаются в двух точках: в точке x = 0, y = 0 и в точке x = 1, y = 1(точки определяются как решение уравнения x = x^2). Получается такой своеобразный "лепесток", площадь которого нам и предстоит вычислить.

Наша задача имеет точное решение. А именно, площадь S указанной фигуры следующая:

Однако мы будем использовать несколько иной подход.

Рис. 1. Вычисление области фигуры, ограниченной двумя кривыми

Метод, который описывается далее и применяется нами для вычисления площади фигуры, имеет отношение к теории вероятностей и математической статистике(обычно такой подход называют методами Монте-Карло).

При вычислении площади фигуры мы будем исходить из следующих соображений. Во-первых, замечаем, что область ограниченная кривыми, полностью попадает в единичный квадрат с левой нижней вершиной в точке начала координат и правой верхней вершиной в точке с единичными координатами. Если мы случайным образом выберем точку внутри этого квадрата, то она с некоторой вероятностью попадает в область, что ограничена кривыми (то есть попадает внутрь "лепестка").

Теория вероятностей утверждает, что эта самая вероятность равна отношению площадей "лепестка" и квадрата. У квадрата с единичной стороной площадь равна единице. Поэтому площадь "лепестка"(которую нам необходимо вычислить) равняется вероятности, с которой случайным образом выбранная точка попадает внутрь "лепестка". Это будет "во вторых".

В третьих, если взять очень много случайных точек, равномерно распределенных по квадрату, и вычислить отношение количества точек внутри "лепестка" к общему количеству точек, в идеале получим оценку, близкую к вероятности попадания случайно выбранной точки внутрь "лепестка".

Мы всю эту процедуру немного модифицируем и поступим следующим образом. Вместо того чтобы генерировать случайны точки, покроем весь квадрат равноотстоящими узловыми точками. Посчитаем, сколько их попало внутрь "лепестка"(то есть области, ограниченной кривыми), и поделим на общее количество точек. Это и будет результат.

Программный код, в котором реализован такой подход, представлен ниже:

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# Количество равных интервалов, на которые
# делятся стороны единичного квадрата
n = 500
# "Цена деления" - расстояние между соседними точками
dz = 1 / n;
# Количество точек, которые попадают внутрь области
pts = 0
# Начальное значение индекса, определяющего столбец точек
i = 0
# Внешний оператор цикла. Перебираем столбцы точек
while i <= n:
    # x - координата точки
    x = dz * i
    # Начальное значение второго индекса для точек столбца
    j = 0
    # Внутренний оператор цикла. Перебираем точки
    # в одном столбце
    while j <= n:
        # y - координата точки
        y = dz * j
        # Условный оператор: проверяем, попала ли точка
        # внутрь области
        if y <= x and y >= x**2:
            # Еще одна точка внутри области
                pts += 1
        # Значение второго индекса увеличиваем на единицу
        j += 1
    # Значение первого индекса увеличиваем на единицу
    i += 1
# Вычисляем площадь фигуры
S = pts / (n + 1) ** 2
# Отображаем результат
print("Площадь фигуры: " + str(S))

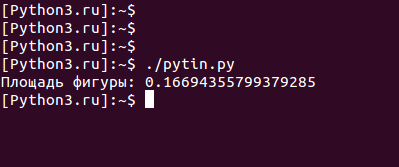
Результат, который приведен ниже, достаточно близок к точному решению:

Чтобы понять логику вычислений, имеет смысл мысленно представить, как мы разбиваем каждую из сторон квадрата на определенное количество интервалов. Количество этих интервалов записывается в переменную n(то есть значение 500).

Границу интервалов будем называть узловыми точками. Через каждую узловую точку на сторонах квадрата проводим горизонтальные и вертикальные линии. Точки пересечений этих линий - это именно те точки, которые нам нужны. Каждую такую точку можно "идентифицировать" с помощью двух индексов.

Первый индекс определяет узловую точку по горизонтали, а второй - узловую точку по вертикали. На пересечении линий, проходящих через эти узловых точки, находится "идентифицируемая" точка внутри квадрата.

Если мы зафиксируем первый индекс, и будем брать разные значения для второго индекса, то все соответствующие точки будут находится на одной вертикальной прямой. Про такие точки будем говорить, что они находятся в одном столбце. Если зафиксировать второй индекс и брать разные значения первого индекса, то все соответствующие точки будут находиться на одной горизонтальной прямой. Про такие точки можем говорить, что они формируют ряд точек.

В каждому ряду и в каждом столбце размещено ровно n + 1 точек ( если учитывать и те точки, что находятся на координатных осях).

Расстояние (по горизонтали или по вертикали) между двумя соседними узловыми точками равняется, очевидно, единице, деленной на количество интервалов, на которые разбивалась каждая из сторон квадрата: такая "цена деления" записывается в переменную dz(значение 1/n). В переменную pts(начальное значение 0) будем записывать количество точек, которые попали внутрь "лепестка".

В условном операторе проверяется условие y <= x and y >= x**2. Это и есть условие попадания точки с координатами X(переменная x) и Y(переменная y) внутрь области, ограниченной кривыми y = x и y = x ^ 2. Чтобы точка попадала в это область, необходимо чтобы одновременно выполнялись два условия. Во-первых, точка должна находиться ниже прямой y = x, а это имеет место, если y <= x (нестрогое неравенство - если мы допускаем, чтобы точка могла оказаться не только ниже прямой, но и непосредственно на прямой.)

Во-вторых, точка должна находиться выше параболы y = x ^ 2 (или на самой параболе - такой вариант мы тоже допускаем). Соответствующее условие выглядит как y >= x ^ 2. Следовательно, должно выполняться соотношение x ^ 2 <= y <= x. Если перевести это на язык Python, то получим y <= x and y >= x**2. Кстати, вместо инструкции y <= x and y >= x**2 вполне законно можно было использовать выражение x ** 2 <= y <= x. Такого типа выражения в Python допустимы.

Начальное значение индекса i , определяющего столбец точек, должно быть нулевым (нулевой индекс соответствует точке на координатной оси). Через первый индекс, напомним, "нумеруются" столбцы точек. Когда запускается внешний оператор цикла, в нем проверяется условие i <=n. Поэтому цикл выполняется до тех пор, пока значение индексной переменной i не превы­сит значение переменной n.

В теле оператора цикла командой x = dz * i вычисляется координата х (вдоль горизонтальной оси - абсцисса) для точек, находящихся в данном столбце (столбец, напомним, определяется значением индекса i ). Также поскольку далее мы планируем перебирать точки в столбце, командой j = О устанавли­ваем начальное ну левое значение для второго индекса, (определяющего по­ложение внутренних точек). После этого выполняется второй, внутренний оператор цикла. В нем проверяется условие j <= n - то есть второй индекс j будет увеличиваться (об этом мы узнаем позже) до тех пор, пока он не пре­высит граничное значение n.

В теле внутреннего оператора цикла командой y = dz * j вычисляется коор­дината у для точки в столбце (координата вдоль вертикальной оси-ордина­та). С помощью условного оператора проверяем, попадает ли точка внутрь "лепестка", и если так, то командой pts += 1 на единицу увеличиваем значение переменной рts (в которую, напомним, записывается количество точек, попадающих внутрь "лепестка").

Перед завершением внутреннего оператора цикла командой j = j + 1 второй индекс увеличивается на единицу. Это последняя команда внутреннего опе­ратора цикла. Внутренний оператор цикла является предпоследней "коман­дой" внешнего оператора цикла. А последняя команда внешнего оператора цикла - это инструкция i += 1 , которой на единицу увеличивается значе­ние первого индекса.

После выполнения внешнего оператора цикла, переменная pts содержит значение количества точек, которые попадают внутрь "лепестка". Общее количество точек, как несложно догадаться, равняется (n + 1) ** 2 (в каждом из n + 1 столбцов по n + 1 точек - всегда (n + 1)^2 точек). Поэтому если мы поделим одно значение на другое, получим площадь "лепестка". Соответствующее значение вычисляется командой S = рts / (n + 1) ** 2. Наконец, командой print отображаем результат.

Интересное видео в тему: